| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- Scratch
- insertion Sort
- 잘 짜인 코드
- 7월4일
- 프로그래밍
- Operating System
- Deep Learning
- 운영체제 강의
- 영어논문
- control flow
- 여행
- 직업으로서의 정치 서평
- CLRS
- 독립기념일
- Process
- scheduling policy
- 푸드트럭
- The beauty and Joy of computing
- xv6
- 균형의 정치
- concurrency
- 스크래치
- 맛집
- Jupyter Notebook
- list
- Lock
- 코딩
- 버클리
- 미국
- Snap!
- Today
- Total
여행다니는 펭귄
Chapter 2. Divide and Conquer (1) 본문
Chapter : CLRS 2.3 4.3~4.6 9
1. Correctness of Merge Sort (1)
2. Running Time Analysis : recurrence relation , Master method , Substitution method (1)
3. Linear time selection (2) Not Today!
Merge Sort와 Selection Sort의 알고리즘만 Jupyter Notebook에서 Code 참조 바람.
Correctness of Merge Sort
이제 Merge Sort Alg의 타당성을 증명하여 보자.
* 알고리즘의 타당성 증명법
| iterative case | non iterative case (recursive) |
| # 1) Find the loop invariant # 2) Define the inductive hypothesis # (internal state at iteration i) # 3) Prove the base case (i=0) # 4) Prove the inductive step (i => i+1) # 5) Prove the conclusion (i=n => correct) |
# 1) Define the inductive hypothesis (correct for inputs of sizes 1 to i) # 2) Prove the base case (i < small constant) # 3) Prove the inductive step (i => i+1 OR {1,2,...,i} => i+1) # 4) Prove the conclusion (i=n => correct) |
Merge Sort는 Recursive 하므로 iterative case가 아니다. 고로 후자를 선택하여 Correctness를 증명하여야 한다.
#1) Inductive Hypothesis
이는 input 된 size의 list가 sorted 되어 있는 경우로 정함.
#2) Basecase
size 가 1일 경우 trivially sorted!
#3) Prove the inductive step
만약 Left list와 Right list가 모두 sorted 되어 있다고 가정하자.
[a_1 a_2 a_3 ... a_n]
[b_1 b_2 b_3 ... b_n]
내부 Merge 하는 Loop가 타당하게 Sorted 된 List를 return하는지 증명해야한다.
여기에선 또 새로운 Loop invariant를 통해서 증명해야 한다.
증명은 Skip 해도 되나, 확인하고 싶다면 ↓
0. Loop invariant
Condition 1. result[0] < result[1] < result[2]....<result[i] 여야 한다.
Condition 2. result[i] < min (left와 right에 남은 원소) 여야 한다.
1. Base Case
첫번째 iteration 후에는
left = [a_0,.....a_n] right = [b_0,......b_n] (left와 right은 sorted 되어 있다.) 에서
a_0과 b_0중 더 작은 것이 들어가게 된다.
result에는 원소가 1개만 존재하므로 result는 trivially sorted 되어있다. 고로 Condition 1을 만족한다.
a_0 < b_0 일 경우 result[0] = a_0이 되고s
left = [a_1..... a _ n] 이고 right = [b_0,...,b_n] 인데
left 는 already sorted 되어 있으므로 result[0] < min( left ) (= a_1) 이고
right의 경우 result[0]( = a_0) < min(right) (= b_0) 이므로 Condition 2를 만족한다.
....(생략)
2단계와 3단계는 직접 증명해 보기
위 증명에 의해 merge가 정렬된 한개의 list를 반환함을 알게 되었다.
고로 두개의 정렬된 list가 있다면 다음 iteration에는 정렬된 하나의 list를 반환한다.
#4) Conclusion
Inductive Hypothesis 가 모든 i에 대해 성립하므로. 어떤 length의 list를 가져오던 mergesort는 sorted 된 리스트를 반환하게 된다.
Running Time Analysis
Recurrence relations
Tree method
Iteration method
Master method
Substitution method
Recurrence Relation
재귀적으로 자신을 call 하는 함수는 점화식을 쓰는 것이 유리하다.
def mergesort(A): #T(n)
if len(A) <= 1:
return A
left = mergesort(A[0:n/2]) #T(n/2)
right = mergesort(A[n/2:n]) #T(n/2)
return merge(left, right) #O(n)mergesort의 경우 재귀적으로 자신을 call 하는 함수 이므로 점화식으로 나타낼 수 있다.


그렇다면 T(n)은 어떻게 계산할 수 있을까?
이를 계산하는 방법인 Tree method , Iteration method, Master method , Substitution method 들이 존재하며
위 방법에 대해 merge sort에 적용하며 알아보도록 하겠다.
Recursion Tree Method

이와 같이 Tree를 그려서 그 레벨에 있는 값을 차례로 더하는 방법을 의미한다.
Merge Sort의 경우 위 그림과 같이 (number of levels) * (work per level) 로 구할 수 있다.

Iteration method

그렇다면 여기서 k는 무엇일까?

T(1) 은 C 이므로

이다.
Master method
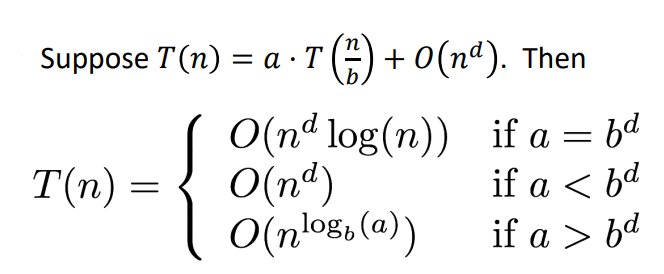
merge sort의 경우 a = 2 b =2 d=1 으로 1번 케이스에 해당하므로

이다.
그렇다면 각각의 Case는 무엇을 의미할지 궁금하지 않은가?
여기에서 세개의 example을 들어 보겠다.



식만 봐서는 무슨 의미인지 잘 보이지 않는다. Tree를 한번 만들어 보자.

첫번째 Case는 아래로 갈수록 가벼워지고 두번째 Case는 아래로 가도 같고 세번째 Case는 아래로 갈수록 무거워진다.
각각의 Case는 Problem의 가중이 어디에 있는지를 의미한다.
Master method는 Tree method와 같은 것을 매우 간편하게 나타낼 수 있지만 Subproblem의 크기가 동일해야만 사용 가능하다.
Substitution Method
substitution method는 사실상 증명법에 가깝다.
1. 추측하기
2. 내 추측이 맞는지 증명해보기
Inductive Hypothesis를 사용해도 좋고 여러 방법을 사용해도 됨
3. 추측 안하고 맞춘 척 하고 증명만 남기기
'컴퓨터 > CLRS' 카테고리의 다른 글
| Chapter 4. Randomized Algorithms (2) (0) | 2021.10.11 |
|---|---|
| Chapter 4. Randomized Algorithms (1) (0) | 2021.10.10 |
| Chapter 3. Linear Time Sorting (0) | 2021.10.03 |
| Chapter1. Algorithmic Analysis (0) | 2021.09.26 |
| Introduction to Algorithms (0) | 2021.09.26 |



